

The Venus Transit 2004
... Extended InfoSheet D1
Venus - The second planet of the solar system
The planet Venus is the second closest planet to the Sun (distance 108 million km or 0.72 AU) and our nearest planetary neighbour. It takes about 225 days to orbit the Sun. Its retrograde rotation of 243 days means that the planet spins from east to west, rather than west to east, as the Earth does. So on Venus the Sun (though invisible through the clouds) rises in the west and sets in the east. This slow retrograde rotation results in Venus' solar day lasting 117 terrestrial days. Like Mercury, Venus has no known natural moon, so we can only measure its mass accurately when a spacecraft passes or orbits it. Venus' mass turns out to be about 0.82 times that of the Earth or 4.9 x 10 24 kg.
Named after the Roman goddess of love and beauty, it is one of the most beautiful objects in the sky. Viewed from Earth, it can outshine every celestial body except the Sun and the Moon. It is the third in brightness and its faint light can cast shadows of objects on the ground at night. Venus at its brightest may be seen in the daytime sky.
An anecdote from the 19th century told by the French astronomer Francois Arago relates how Napoleon visited a midday party, which had been arranged in his honour. On his arrival he was ignored by the hosts because they were looking up at the sky. He asked angrily why he was shown such disrespect and was amazed to hear that the hosts, in spite of it being noon, were looking for a star which they attributed to the conqueror of Italy. After Napoleon had seen the shining dot with his own eyes, he was deeply moved by the dedication.

Friedrich: Mann und Frau betrachten den Mond
The Babylonians first recorded the appearance of Venus nearly 4000 years ago. As an inferior planet, it appears to oscillate about the Sun and is never seen more than 48 degrees on either side of it. So they thought Venus to be two separate bodies - a morning star rising just before sunrise and an evening star setting just after sunset. The ancient Greeks called the morning star Phosphorus and the evening star Hesperus. About 500 BC, the Greek scientist/philosopher Pythagoras recognized that the two "stars" were actually the same body.
There are three reasons for the brightness of Venus. Two of them - its closeness to Earth, which can be as little as 40 million kilometres and its relatively large diameter (12,104 kilometres), which is only a little less than the diameter of the Earth (about 5 percent) - make Venus a suitable object for astronomical research. But the third reason makes Venus a nightmare for astronomers - the planet is covered by a dense unbroken shell of clouds.

Venus' clouds seen from MARINER 10
This cloud cover completely frustrates any attempt to view the planet's surface through optical telescopes. The Italian astronomer Galileo Galilei was the first to observe Venus telescopically. He discovered that it displays phases similar to those of the Moon and that it changes its apparent size over a continually recurring cycle. So he became convinced that Venus revolves around the Sun. Thus he realized that the Sun is the centre of revolution of all the planets and that the Copernican model of the universe is correct.

Photo sequence of the Venus phases
Even under the most favourable viewing conditions, Venus appears unimpressive and almost featureless in a telescope. The few observable features consist of small differences in colour as shown in the unusual photograph taken at the New Mexico State University. Quite often the cusps appear brighter than the rest of the crescent, and a narrow strip along its entire limb appears brighter when the planet is in the crescent phase. There is also a darkening effect along the illuminated edge of the terminator (the line of demarcation between the bright and dark parts of the face of Venus).

Cloud structure of Venus in ultraviolet light
The only way to penetrate the completely cloud-covered atmospheric shell is to beam radar waves to the surface or send a spacecraft to the Venusian surface. The first ground-based radar investigations were made in the mid-1970s with the giant 310-metre antenna at Arecibo in Puerto Rico with a resolution of 12 cm. Later, American and Russian spacecraft orbited the planet and not only did they scan its surface with radar, radio, ultraviolet and infrared detectors but some of them plunged onto its forbidding surface to radio back information about atmospheric and surface conditions.
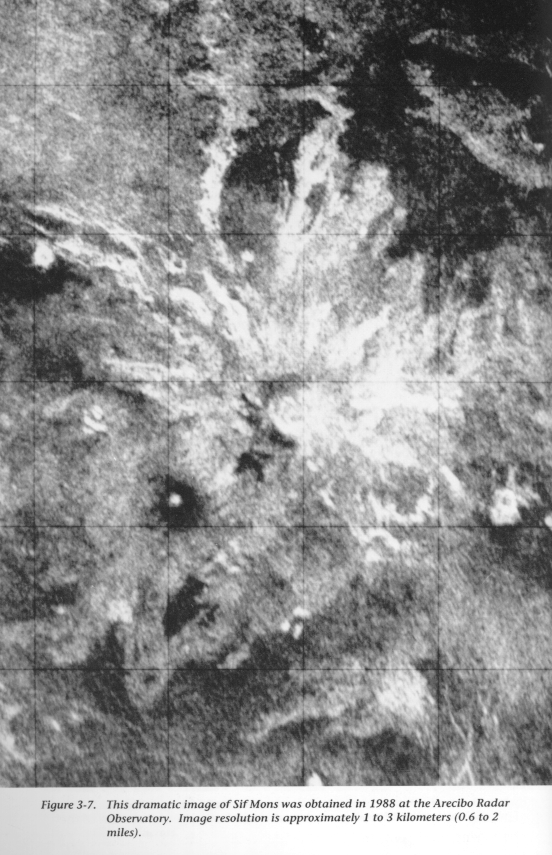
Radar map taken by the Arecibo observatory
Astronomers refer to Venus as Earth's sister planet, because both are similar in size, mass, density and volume. Both formed about the same time and condensed out of the same nebula. So before 1961 many people supposed that Venus might be Earth-like and might even have life-forms on its surface
However, during the last few years scientists have found that Venus is very different from the Earth. It has no oceans and it is surrounded by a dense atmosphere composed mainly of carbon dioxide with virtually no water vapour. Its clouds are composed of sulphuric acid droplets. At the surface, the atmospheric pressure is 92 times that of Earth's at sea-level and it is scorched by a temperature of about 482 degrees Celsius. This high temperature is primarily due to a runaway greenhouse effect. Sunlight passes through the atmosphere to heat the surface of the planet. Heat is radiated, but it is trapped by the dense atmosphere and is not allowed to escape into space. This makes Venus hotter than Mercury. Because Venus is so hot, it is extremely unlikely there is any possibility that life has formed there.
Physical data / Planet statistics
| Mean distance from the Sun (km) | 108.200.000 |
| Orbital period (days) | 224.701 |
| Orbital inclination (degrees) | 3.394 |
| Orbital eccentricity | 0.0068 |
| Tilt of axis (degrees) | 177.36 |
| Rotational period (days) | 243.02 |
| Equatorial radius (km) | 6 051.8 |
| Mass (kg) | 4.689 X 10 24 |
| Mass (Earth = 1) | 0.811476 |
| Mean density | 5.25g/cm 3 |
| Visual geometric albedo | 0.65 |
| Magnitude (Vo) | -4.4 |
| Mean surface temperature | 482°C |
| Atmospheric pressure (bars) | 92 |
Atmospheric composition
| 96% 3+% |
Go to the corresponding Brief InfoSheet
Back to the List of Extended InfoSheets.



