The Venus Transit 2004
... Extended InfoSheet B1
Predictions of the Venus transit of June 8, 2004 [1]
We give in this document the predictions of the Venus transit in front of the Sun of June 8, 2004. These predictions are made using planetary theories VSOP87 made at IMCCE; the accuracy of the positions of interior planets in these theories is about 0,005 second of degree. Obtaining the apparent co-ordinates of the stars require the use of theories of the precession and nutation and the sidereal time. We used the theory of the precession of Lieske (1976), the theory of the nutation of Wahr (1981) and the sidereal time of Aoki (1992). These predictions also depend on a certain number of physical parameters which must be coherent between them and with the planetary theories used. As theories VSOP87 use the value of the astronomical unit of the UAI 1976 (= 149 597 870 km have ) we also used the constant UAI 1976 for the terrestrial equatorial semi-diameter (R = 6378,140 km) and for the value of the mean horizontal equatorial parallax of the Sun (p 0 = 8.794148"= R/a). We also took the constants UAI 1976 for the solar semi-diameter seen at one astronomical unit (D = 15' 59,63") and for the Venus semi-diameter (d' = 6051.8 km). The flatness of the Earth is taken equal to 1/298,257 (IERS 1992). For these calculations, as for the making of our canons of transits of Mercury and Venus, we used formulae identical to that of the solar eclipses using the elements of Bessel.
There are three types of information : general circumstances of the transit, geocentric circumstances of the transit and finally local circumstances of the transit. In all the cases the time scale used in the predictions is the coordinated universal time (UTC or UT), the difference between terrestrial time (TT) and the coordinated universal time (TT-UTC) was taken equal to 65,184s.
In our tables, geographical longitudes are always counted positively towards the west and negatively towards the east.
General circumstances
One gives the characteristics of the conjunction in longitude between Venus and the Sun: it is the moment when the geocentric apparent longitudes of Venus and the Sun are equal. The general circumstances of the transit describe the contacts of the terrestrial ellipsoid with the edges of the cones of penumbra and shadow. Each contact thus corresponds to a particular place and to a particular moment. This place of the terrestrial surface is the point of tangency between the ellipsoid and the cone of shadow or penumbra at the time of the contact. The maximum of the contact corresponds to the moment and the place on Earth, where the distance between this place and the axis of the cones is minimal ; this place has Venus at the horizon at the moment considered. We also give for each contact the place on Earth which has Venus (or Sun) at its zenith, this direction allows to trace the circle of visibility of Venus at the moment considered.
| Conjunction on June 8, 2004 at 8h 43m 4.97s UTC. | |
| Geocentric longitude of Venus | 77° 53' 20,783 |
| Geocentric latitude of Venus | -0° 10' 34,42" |
| Geocentric longitude of the Sun | 77° 53' 20,783" |
| Geocentric latitude of the Sun | -0° 0' 0,60" |
| Equatorial parallax of the Sun | 8,66" |
| Equatorial parallax of Venus | 30,44" |
| True semi-diameter of the Sun | 15' 45,4" |
| True semi-diameter of Venus | 28,88" |
The apparent Venus diameter is three hundredth of the apparent diameter of the Sun.
General phases
| Phases | Date in UTC | Position of the contacts | Place having the planet at the zenith | ||
| Longitude | Latitude | Longitude | Latitude | ||
| First contact of the penumbra | 5h 6m 30,5s | +177° 25,7' | -23° 12,9' | -103° 24,1' | +22° 45,4' |
| First contact of the shadow | 5h 25m 27,4s | -176° 27,6' | -25° 52,1' | -98° 38,6' | +22° 45,2' |
| Maximum of the transit | 8h 19m 44,3s | -86° 39,9' | -63° 29,9' | -54° 52,4' | +22° 43,1' |
| Last contact of the shadow | 11h 13m 58,9s | +48° 52,7' | -49° 30,5' | -11° 6,8' | +22° 41,0' |
| Last contact of the penumbra | 11h 32m 56,0s | +56° 11,2' | -47° 8,5' | -6° 21,3' | +22° 40,7' |
Durations of the general phases
Duration of the general transit: 6h 26m 25,45s.
Duration of the transit in the shadow: 5h 48m 31,49s.
Physical parameters of the cones of shadow and half-light and minimal elongation
Radius of the cone of shadow: 42,08 terrestrial radii.
Geocentric distance to the edge of the shadow: 13,30 terrestrial radii.
Geocentric distance of the edge of the penumbra: 15,95 terrestrial radii.
Radius of the cone of penumbra: 44,73 terrestrial radii.
Topocentric minimal distance between the centres of the Sun and Venus: 10' 5,156".
Geocentric circumstances
The geocentric circumstances are related to a quite particular point : the centre of the terrestrial ellipsoid. We provides the moments of the various contacts, these moments corresponding to the moments when, seen from the centre of the Earth, the apparent disc of Venus is tangent outside or inside the solar disc. They are also the moments when the centre of the Earth enters and leaves the cones of shadow and penumbra. The maximum of the transit is the moment when, always seen from the centre of the Earth, the distance between the centres of Venus and the Sun is minimal.
As for the general circumstances, we provide also the places on the terrestrial surface having Venus to its zenith at the time of the contacts. We provide for each contact, the angle with the pole of the contact, it is the angle between the segment joining the centre of the Sun and the point of contact on the solar limb and the direction of the north celestial and counted positively starting from north towards the east (figure 1).
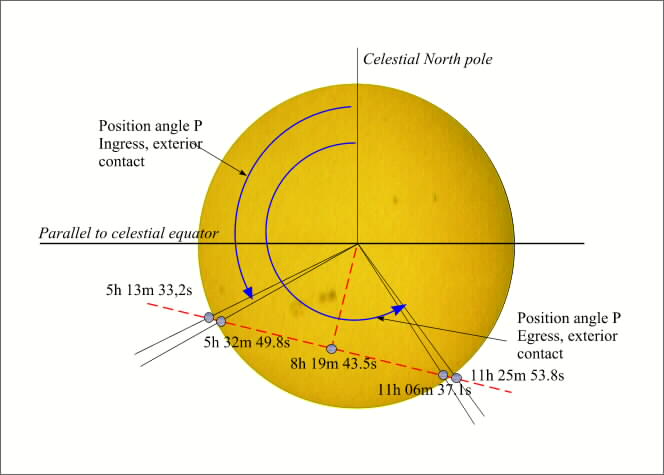
Figure 1. - Geocentric Circumstances.
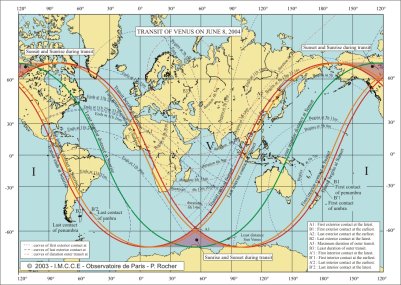
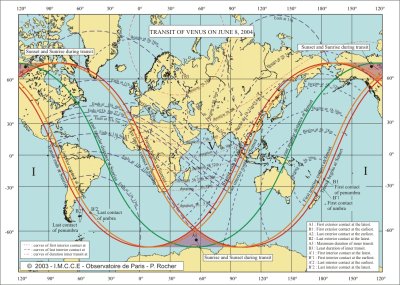
| Geocentric phases | Moment in UTC | Place having the planet at the zenith | Polar Angle | |
| Longitude | Latitude | |||
| First external contact | 5h 13m 33,2s | -101° 37,9' | +22° 45,3' | +116° 15,7' |
| First interior contact | 5h 32m 49,8s | -96° 47,5' | +22° 45,1' | +119° 22,7' |
| Maximum of the transit | 8h 19m 43,5s | -54° 52,6' | +22° 43,1' | --- |
| Last interior contact | 11h 6m 37,1s | -12° 57,8' | +22° 41,0' | +213° 13,2' |
| Last external contact | 11h 25m 53,8s | -8° 7,3' | +22° 40,8' | +216° 20,2' |
Durations of the geocentric phases
Duration of the general transit: 6h 12m 20,68s.
Duration of the transit in the shadow: 5h 33m 47,26s.
Minimal geocentric angular distance: 10' 26,875".
Remarks
The durations of the geocentric phases are shorter than the durations of the general phases, this difference corresponds to the time taken by the edges of the cones of shadow and penumbra to cross a terrestrial radius.
The difference between the minimal geocentric angular distance and the minimal topocentric angular distance corresponds to the difference in parallax between the centre of the Earth and a place seeing the minimum at the horizon, therefore the two bodies close to the horizon. This difference must thus be of the order of the differences between the equatorial horizontal parallaxes of Venus and the Sun. In fact we have 10' 26,875"- 10' 5,156" = 21,719" and the difference of the true equatorial parallaxes (at the moment of the conjunction) is 30,44" - 8,66"= 21,78".
Local circumstances
The local circumstances are in all points similar to the geocentric circumstances but they are referred to a particular place. We will not give here the local circumstances for many places on the surface of the Earth, because of the lack of place and also because we do not want to influence the measurements that you wish to make. We give the values, for each contact, of the coefficients E, F and G described in the preceding sheets. These coefficients make possible to calculate the approximate values of the contacts in any place from the moments of the geocentric contacts.
| Phase | E | F | G |
| First external contact | 6,4823 min | -0,0556 min | 2,8992 min |
| First interior contact | 6,6111 min | 0,6731 min | 3,3721 min |
| Last interior contact | 3,2893 min | 3,4236 min | -5,7456 min |
| Last external contact | 2,8106 min | 3,8404 min | -5,2725 min |
The variation with the moments of the geocentric contacts is given by the following formula :
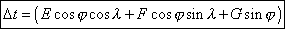 (1)
(1) where λ and φ represent the longitude and latitude of the place of observation.
Example : Calculation of the local circumstances for Paris :
The geographical co-ordinates of Paris are as follows :
Latitude : 48° 50' 11,2" North = 48.8364°
Longitude : -2° 20' 13,8" (East) = -2.3372°
| Topocentric contacts | ΔT calculated using the formula (1) | Date calculated using the formula (1) | Dates calculated using the exact formulae |
| First external contact | 6,4474 min | 5h 20m 0,0s | 5h 20m 6,1s |
| First interior contact | 6,8685 min | 5h 39m 41,9s | 5h 39m 48,3s |
| Last interior contact | -2,2539 min | 11h 4m 21,9s | 11h 4m 20,8s |
| Last external contact | -2,2237 min | 11h 23m 40,4s | 11h 23m 39,9s |
It is noted that the differences between the approximate values and the computed values with the rigorous formulas, therefore without approximation, are of the order of the tenth of a minute.
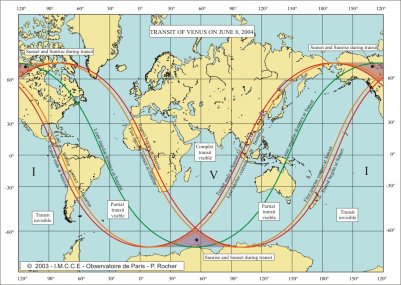
Charts of visibility
These charts are made using the projection of Mercator. This traditional projection in geography, made by Mercator in 1569, has the name of projection wrongly: it actually is a cylindrical conform development. This projection is well adapted to the navigation at sea because the routes at constant azimuth are then as lines. Unfortunately, the enlarge the latitudes when going towards the poles. Circles are then not represented by circles but by curves elongated towards the poles.
The drawing of the charts has been made using the software GMT (Generic Mapping Tools Graphics) made by Paul Wessel (School of Ocean and Earth Science and Technology, University of Hawaï at Manoa) and Walter. H. F. Smith (Laboratory for Satellite Altimetry, NOAA/NESDIS/NODC).
We give three charts: a chart of visibility showing the limits of visibility of the phenomenon. We are close to the beginning of the summer in the northern hemisphere, it thus exists a zone close to the northern terrestrial pole with no sunset, the totality of the transit is then visible in this zone but the Sun is low on the horizon. On the contrary, near the southern terrestrial pole, there is a zone where there is no sunrise, the transit is thus invisible there. One will also notice two zones, one in the south where the Sun will rise then set and one in north where the Sun will set and rise during the transit. The second chart is identical to the first, but shows also three types of curves, the curves of beginning and end of the transit at a given moment and the curves of equal durations for the total transit. The curves beginning and ending at a given moment correspond to the places on Earth where the external contacts take place at the same moment. The curves of equal durations correspond to the places on Earth where the totality of the transit, i.e. the difference in time between the last and the first external contacts is equal. It is noticed that these curves are not parallel to the meridian lines. The third chart is identical to the second, but, the curves of beginning and end of the transit at a given moment and the curves of equal durations of the transit correspond to the interior contacts and to the duration of the interior transit.
The phenomenon to be observed
From any place in the zone of complete visibility of the phenomenon, an observer will attend the transit of the disc of Venus in front of the solar disc. The apparent trajectory of the Venus on the disc of the Sun will depend on two things:
- the place of observation since we will take advantage of the observed difference to determine the parallax
- the frame in which we observe. Indeed, if one uses an equatorial reference frame (telescope on an equatorial mounting according to the Sun in its diurnal movement) the Venus trajectory is quasi-rectilinear. So on the other hand, if one uses an azimuth reference frame (solarscope, venuscope or any system of projection on a fixed screen referring to the zenith of the observational place), the trajectory of Venus will be more complex. That is why we provide two parameters useful for the determination of the points of contacts of the transit:
- the polar angle "P" of a contact (this is the angle having for summit the centre of the Sun and for sides the direction of the celestial North Pole and the direction of the contact. It is counted positively towards the East starting from the direction of the pole).
- the angle with the zenith "Z" of a contact (this is the angle having for summit the centre of the Sun and for sides the direction of the zenith of the place and the direction of the contact. It is counted positively towards the East starting from the direction of the zenith).
One gives below the local circumstances and the observable trajectories as seen from Paris for these two types of observation.
Paris : latitude : 48°51'54.18" N; longitude : 2°20'59.16" E.
| UT | P | Z | |
| First external contact | 5h 20m 6.0s | 117.7° | 159.8° |
| First internal contact | 5h 39m 48.2s | 121.0° | 164.2° |
| Last internal contact | 11h 4m 20.6s | 212.4° | 228.9° |
| Last external contact | 11h 23m 39.7s | 215.6° | 225.4° |
Duration of the central phase : 5h 24m 32.4s,
of the general phase: 6h 3m 33.7s.
Characteristics of the maximum of the transit : Instant of the maximum : 8h 22m 53.4s and minimum of distance : 10' 40,9"
Elevation of the Sun above the horizon : 42° and azimuth: 284°
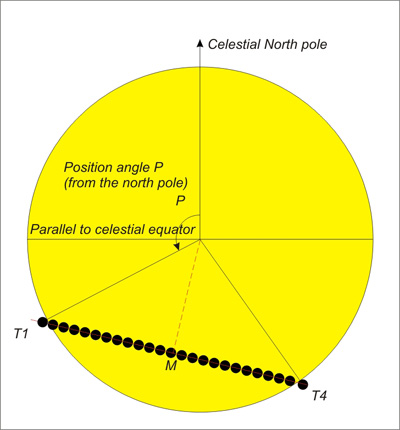
Figure 2 : Aspect of the trajectory of Venus as seen from Paris in the equatorial reference frame, for example seen in a telescope with an equatorial mounting.
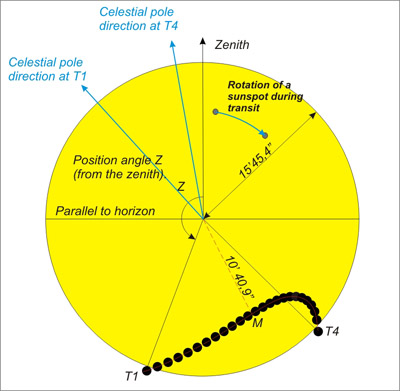
Figure 3: Aspect of the trajectory of Venus as sen from Paris in the horizontal reference frame, for example seen in a solarscope.
Go to the corresponding Brief InfoSheet
Back to the List of Extended InfoSheets.