Fitting of data

The final step in data reduction is the extraction of astrophysical parameters from the data. This is often done by fitting a parameterized model of the objects to the data by means of least squares and maximum likelihood methods (see Section 2.1.3). The correct weighting of data is important in order to use all information in the image and minimize the effects of noise on the final parameters. For stellar images or line profiles, either analytical functions (e.g. weighted Lorentzian-Gaussian profiles) or empirical models of the PSF are used to obtain flux and shape parameters. Very elaborate models may be applied to more complex objects such as galaxies where the flux are decomposed in a set of different components e.g. bulge, disk, bar and spiral.

When a set of objects have similar features and their relative shifts should be determined, the correlation between them and a template object Tis analyzed using the cross-correlation function :

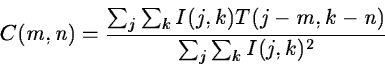$$C(m,n) = \frac{\sum_j \sum_k I(j,k)T(j-m,k-n)}{\sum_j \sum_k I(j,k)^2}$$ (2.31)

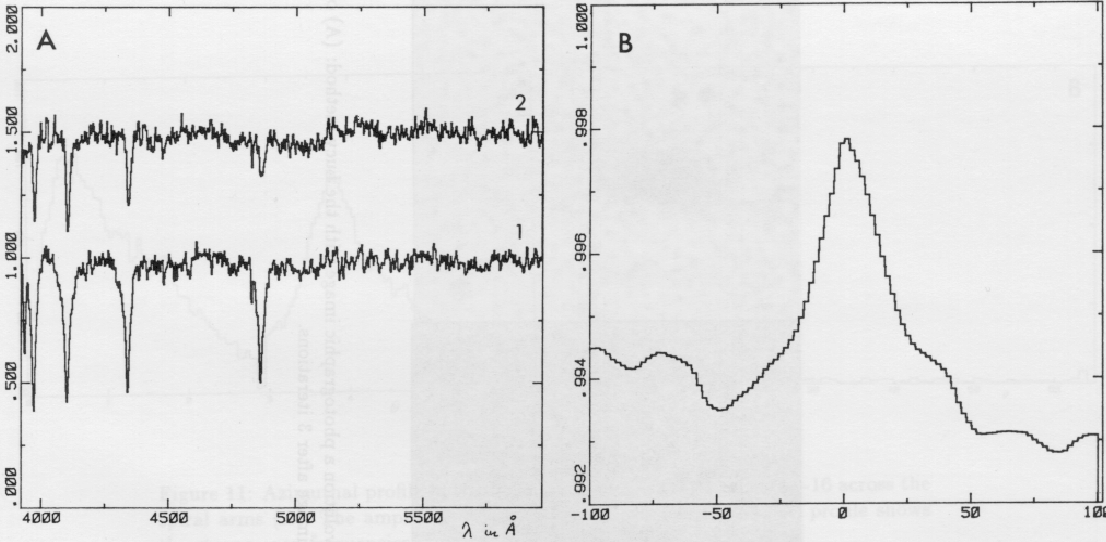
where I is the object. Since this function is 1 for a perfect match between object and template, the maximum value will indicate how similar the objects are. The location of the main peak gives the translation and is used in spectroscopy to determine radial velocities of stars. This is shown in Figure 2.12 where the normalized spectra of two early type stars are cross-correlated. Since only the spectral lines should be used, it is important to subtract or normalize the continuum to avoid interference from it.

  

Figure 2.12: Two normalized early type spectra used as template (A1) and object (A2) yield the cross-correlation function (B).