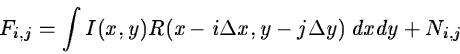Image sampling

The acquisition of a data frame involves a spatial sampling and digitalization of the continuous image formed in the focus plane of a telescope. The image may be recorded analog (e.g. on photographic plates) for later measurements or acquired directly when digital detectors such as diode arrays and CCD's are used. The individual pixel values are obtained by convolving the continuous image I(x,y) with the pixel response function R(x,y). With a sampling step of $\Delta x$ and $\Delta y$ the digital frame is given by

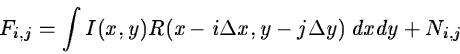$$F_{i,j} = \int I(x,y) R(x-i\Delta x, y-j\Delta y) \; dx dy + N_{i,j}$$ (2.1)

where N is the acquisition noise. This convolution is done analog in most detectors except for imaging photon counting systems where it partly is performed digitally. The sampling step and response function are determined normally by the physical properties of the detector and the acquisition setup. The variation of the response function may be very sharp as for most semi-conductor detectors or more smooth as in image dissector tubes. If the original image I is band width limited (i.e. only contains features with spatial frequencies less than a cutoff value $\omega_c$) all information is retained in the digitized frame when the sampling frequency $\omega_s = 2\pi/\Delta x$ satisfies the Nyquist criterion:

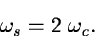$$\omega_s = 2 \; \omega_c.$$ (2.2)

In Equation 2.2 it is assumed that R is a Dirac delta function. This means that only features which are larger than $2\Delta x$ can be resolved. A frame is oversampled when $\omega_s > 2\omega_c$ while for smaller sample rates it is undersampled.

In astronomy the band width of an image is determined by the point spread function (PSF) and has often no sharp cutoff frequency. Many modern detector systems are designed to have a sampling step only a few times smaller than the typical full width half maximum (FWHM) of seeing disk or PSF. Therefore they will not fully satisfy Equation 2.2 and tend to be undersampled especially in good seeing conditions.

A typical assumption in image processing algorithms is that the pixel response function R can be approximated by a Dirac delta function. This is reasonable when the image intensity does not vary significantly over R as for well oversampled frames where the effective size of Ris roughly equal to the sample step. If it is not the case, the effects on the algorithm used should be checked. Interpolation of values between existing pixels is often necessary e.g. for rebinning. Depending on the shape of R and band width of the image different schemes may be chosen to give the best reproduction of the original intensity distribution. In many cases low order polynomial functions are used (e.g. zero or first order) while sinc, spline or gaussian weighted interpolation may be more appropriate for some applications.