The problem of deciding the height of the telescope pier is frequently one of the most controversial in the design of the observatory facility. On the one hand one would like to set the telescope out of the possibly negative effects of the ground proximity. On the other hand the cost of the building increases rapidly for every additional meter of height: first the cost of concrete, steel and handling equipment needed for a higher building, and later the additional time and effort required for every handling operation, from the initial assembly of telescope and dome to the regular maintenance handling of mirrors and instruments.
When ample funds were available, the opinion of designers tended to be
quite prudent and conservative with regard to the possibility of
seeing from the near-ground layer and the telescope
support was set as high as practical (which in many cases was about 30
meters). When budgets were limited, telescopes were set at more modest
heights and eventually the feared consequences on seeing
quality did not materialize or anyway were not quantified.
The case of the ESO 2.2-m telescope mentioned
earlier in section 
is quite typical in this
respect.
In reality the optimal height for a telescope
from the standpoint of seeing quality
will depend on the overall optical performance aimed for the
telescope as well as of the particular phenomena in the near ground
atmospheric layer, which may vary at different sites and also
within particular locations of a same mountain site.
For a modern technology large telescope which aims at a overall
FWHM quality of the order of 0.5 arcsec,
it will generally be desirable that the mean seeing
contribution of the near-ground layer does not exceed about
0.1 
0.15 arcsec.
A less ambitious telescope will accept easily 0.2 
0.3 arcsec
from the near-ground layer without significant loss of
performance
.
The local conditions of the surface layer on astronomical sites during
night-time will of course vary but generally share two important
characteristics: the turbulence intensity is low and the ground
surface experiences a strong radiative cooling. Therefore the
temperature gradient in the local surface layer is generally stable
and we have seen (cf. page ) that in those
conditions the seeing will increase when the turbulence is augmented.
The seeing in the surface layer can be evaluated by means
of measurements
of the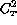 
coefficient at a few points along the vertical of the site.
From the interpolated profile 
the
equivalent seeing FWHM can then be computed by equation
().
Fig. shows some averaged profile reported from
different sites.
All these profiles were measured on "virgin" locations, during the site selection studies of new telescope projects. It may therefore be interesting to analyze the profiles on an already built observatory.
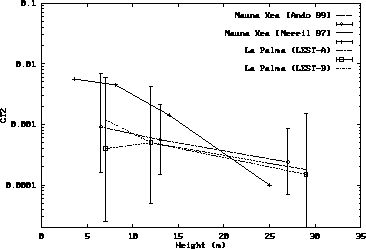
Figure: Some reported 
profiles from different observatories
.
[4]The data from La Palma are from the site survey study for the LEST solar telescope [Ortolani 91].
Systematic recordings of the temperature structure coefficient 
at the La Silla
observatory were taken by the author during
11 consecutive nights from Nov 20
1986. The 
measurements
were taken by special micro-thermal sensors developed at ESO and
described in [Sarazin 92], located at three heights
(10, 20 and 30 meters) on the La Silla main meteo tower (see
fig. , on the left hand). The tower is located on the
leeward edge of a roughly flattened ridge about 50 m wide, well
exposed to the prevailing north winds of La Silla and not directly
in the wake of the other domes built nearby on the ridge. There is also an
asphalted road just upstream of the tower and therefore
the test location may be
taken as a reasonable example of a built site.
The wind was about 5 
6 m/s during the measurement nights, which
also corresponds to the yearly night-time average at La Silla.
The 
data were averaged over periods of one
hour and cover 70 hours of astronomically useful night-time.
Short periods of cloudiness which occurred during
some of the nights were taken out of the data set.
The values
recorded at the height of 10 m are generally higher than those at 20
meters, which are very similar to the values for
30 meters as can be seen by the statistical summary
shown in table .
Table: Statistical summary of night-time
data.
A further analysis suggested that the difference 10-20 meters
was linked to the wind velocity. This is well shown in
fig. , showing a plot of the ratios
and
versus the mean wind velocity.
One can may recognize two ranges of wind velocity:
a range of low winds up to
about 10 m/s where the means of
and
are
respectively about 10
and 
K
m
and the range beyond 12 m/s
where 
is about 
K
m
at all heights.
Thus strong winds mix the surface layer such that
does not depend on the height from the ground.
Fig. shows the values evaluated for each set of
measurements of the integral
with 
as respectively 10, 15 and 20 meters, assuming a linear
variation of 
. The equivalent seeing values
are given in the table below.
Table: Statistical summary of integrated FWHM (arcsec) from height
It appears that the 
values measured in this case are
significantly greater than those of fig. , although
they are by no means alarming in absolute terms: a typical requirement
that the mean seeing
contribution of the near-ground layer does not exceed about
0.15 arcsec, would place the height of the opening (slit) of the telescope
enclosure at about 11 m.
