



Next: Seeing tests on
Up: Experimental studies
Previous: Experimental studies
The experiment described here was performed by the author in
the ESO optical laboratory.
The experiment is
schematically illustrated in fig.  : a parallel laser
beam with a diameter of 3 cm is reflected on a flat horizontal mirror
of a diameter of 4 cm and focused on a position sensing detector (PSD).
The mirror was heated by self-adhesive film resistances
in order to produce seeing which was evaluated from the
rms of
the image motion on the PSD and converted in terms of equivalent FWHM.
: a parallel laser
beam with a diameter of 3 cm is reflected on a flat horizontal mirror
of a diameter of 4 cm and focused on a position sensing detector (PSD).
The mirror was heated by self-adhesive film resistances
in order to produce seeing which was evaluated from the
rms of
the image motion on the PSD and converted in terms of equivalent FWHM.

Figure: Optical schematic of the mirror seeing experiment.
We use here the expression, reported by [Sarazin 92],
relating the variance of short-exposure angular image motion
to Fried's parameter 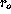 for the long exposure:
for the long exposure:

where  is the wavelength, in the presently case 680 nm,
and D the beam aperture of 3 cm.
Noting that only the variance along one direction was measured on the
PSD:
is the wavelength, in the presently case 680 nm,
and D the beam aperture of 3 cm.
Noting that only the variance along one direction was measured on the
PSD:

one obtains:

where f is the focal distance on the PSD, which was 30 cm in this
experiment.
 was computed from the image motion data recorded by the PSD
over an integration time of about
30 seconds.
was computed from the image motion data recorded by the PSD
over an integration time of about
30 seconds.
The value for the full width half maximum 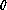 is then evaluated
by equation (
is then evaluated
by equation ( ):
):


Figure: The test mirror on steel plate, itself laid on
the floor of the laboratory.

Figure: The cardboard dome.
Different power settings of the heating resistances fixed around the mirror
were set and the corresponding temperature of the mirror surface
was measured by means of
a contact thermometer. Because of the heating method, the temperature of the
mirror is not completely homogeneous so the values given in the table of
results below represent
averages with an accuracy of a few percents of the mirror-air  .
.
The resolution of the PSD used is about 3 m, which
corresponds to a computed seeing (FWHM) of about
1.3 arcsec. Therefore, in order to get seeing measurements with good
resolution, the mirror was heated up to a
m, which
corresponds to a computed seeing (FWHM) of about
1.3 arcsec. Therefore, in order to get seeing measurements with good
resolution, the mirror was heated up to a  of 100 K.
of 100 K.
The tests were performed in two configurations:
- In the first configuration the mirror was simply laid on the
floor of the laboratory, in "open air" - fig.
 .
.
- The second configuration consisted in having the mirror enclosed
by an octagonal cardboard dome of diameter 30 cm
and a 6-cm wide slit as shown in fig.
 .
.

Figure: Power spectrum of the image motion.
Results
For all tested configurations (which included presence/absence of dome
and different mirror-air  ), seeing measurements were taken
continuously over a period of typically half-hour, sometimes longer.
From these sequences the mean and rms values were then obtained.
), seeing measurements were taken
continuously over a period of typically half-hour, sometimes longer.
From these sequences the mean and rms values were then obtained.
A summary of the main test results for both open-air and dome
configurations is found in the table below.

Table 1: Summary of test results.
1) External disturbances minimized.
The use of equation ( ) to evaluate the results in
terms of FWHM or image size assumes that the turbulence follows
Kolmogorov's law. In order to verify this point, power spectra of the
image motion have been computed on the 30-sec sequences.
As the example of fig.
) to evaluate the results in
terms of FWHM or image size assumes that the turbulence follows
Kolmogorov's law. In order to verify this point, power spectra of the
image motion have been computed on the 30-sec sequences.
As the example of fig.  shows, the spectrum have
clear Kolmogorov's characteristics with an inertial range with slope
shows, the spectrum have
clear Kolmogorov's characteristics with an inertial range with slope
 .
.
A fact apparent from these results is that the dome
configuration starts showing seeing at lower  s than the
open-air one:
however for larger
s than the
open-air one:
however for larger  s the results are quite the same.
It looks like there is an anticipated stable-to-unstable transition
in the dome due to interaction of the mirror convective flow with
the internal dome surface, most likely linked to the tiny geometrical
scale of the model.
Therefore no undue extrapolation of these curious results
should be done to full scale.
s the results are quite the same.
It looks like there is an anticipated stable-to-unstable transition
in the dome due to interaction of the mirror convective flow with
the internal dome surface, most likely linked to the tiny geometrical
scale of the model.
Therefore no undue extrapolation of these curious results
should be done to full scale.
Another important feature shown by the
measurements is the large scattering of seeing values recorded during
a same measurement sequence.
This variability depended very much on the "room turbulence" caused
by the presence of the experimenters and by other external
disturbances, such as opening and
closing a door, happening during a measurement sequence.
One should remark here that the air motions in the generally very
quiet optical lab, which could be caused by
people occasionally moving some meters from the experiment, are very
small in absolute terms and certainly not of turbulent nature.
Nevertheless when such tiny air motions interact with the
convective flow from the mirror, they apparently cause strong
increases of seeing.
One should underline that this increase of seeing values appears
to be clearly due
to some interaction of the "room turbulence"
(which, as said, is not really one) with the convection flow
immediately above the
mirror and is not a purely added "room seeing" effect. If the mirror is
not heated, the "room turbulence" produces no measurable seeing effect.
This indicates the
extreme sensitivity of seeing caused by natural convection to even minimal
air motions and turbulence that have an external cause.
Typically at full scale,
this would correspond to the often reported case of seeing
allegedly caused by leaving a door open on the observing floor in a
telescope dome.

One can also remark that "room turbulence" affects to a proportionally
larger extent the seeing of a mirror with a small  ,
which creates weak convective
flows. Stronger convective flows from larger
,
which creates weak convective
flows. Stronger convective flows from larger 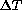 s
tend to predominate over external disturbances.
Some subsequent measurements were taken outside of working hours
in order to minimize disturbances that may affect "room turbulence",
which resulted in sequences - noted with 1) -
with substantially less mean seeing and variability.
Fig.
s
tend to predominate over external disturbances.
Some subsequent measurements were taken outside of working hours
in order to minimize disturbances that may affect "room turbulence",
which resulted in sequences - noted with 1) -
with substantially less mean seeing and variability.
Fig.  shows two comparisons between couples of
sequences taken in the same test configurations.
shows two comparisons between couples of
sequences taken in the same test configurations.




Next: Seeing tests on
Up: Experimental studies
Previous: Experimental studies
Lorenzo Zago, zago@elgc.epfl.ch,
Sun Feb 26 22:57:31 GMT+0100 1995
 : a parallel laser
beam with a diameter of 3 cm is reflected on a flat horizontal mirror
of a diameter of 4 cm and focused on a position sensing detector (PSD).
The mirror was heated by self-adhesive film resistances
in order to produce seeing which was evaluated from the
rms of
the image motion on the PSD and converted in terms of equivalent FWHM.
: a parallel laser
beam with a diameter of 3 cm is reflected on a flat horizontal mirror
of a diameter of 4 cm and focused on a position sensing detector (PSD).
The mirror was heated by self-adhesive film resistances
in order to produce seeing which was evaluated from the
rms of
the image motion on the PSD and converted in terms of equivalent FWHM.





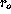 for the long exposure:
for the long exposure:

 is the wavelength, in the presently case 680 nm,
and D the beam aperture of 3 cm.
Noting that only the variance along one direction was measured on the
PSD:
is the wavelength, in the presently case 680 nm,
and D the beam aperture of 3 cm.
Noting that only the variance along one direction was measured on the
PSD:


 was computed from the image motion data recorded by the PSD
over an integration time of about
30 seconds.
was computed from the image motion data recorded by the PSD
over an integration time of about
30 seconds. 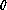 is then evaluated
by equation (
is then evaluated
by equation (


 .
.
 m, which
corresponds to a computed seeing (FWHM) of about
1.3 arcsec. Therefore, in order to get seeing measurements with good
resolution, the mirror was heated up to a
m, which
corresponds to a computed seeing (FWHM) of about
1.3 arcsec. Therefore, in order to get seeing measurements with good
resolution, the mirror was heated up to a  of 100 K.
of 100 K.

 ), seeing measurements were taken
continuously over a period of typically half-hour, sometimes longer.
From these sequences the mean and rms values were then obtained.
), seeing measurements were taken
continuously over a period of typically half-hour, sometimes longer.
From these sequences the mean and rms values were then obtained.

 .
.
 s than the
open-air one:
however for larger
s than the
open-air one:
however for larger  s the results are quite the same.
It looks like there is an anticipated stable-to-unstable transition
in the dome due to interaction of the mirror convective flow with
the internal dome surface, most likely linked to the tiny geometrical
scale of the model.
Therefore no undue extrapolation of these curious results
should be done to full scale.
s the results are quite the same.
It looks like there is an anticipated stable-to-unstable transition
in the dome due to interaction of the mirror convective flow with
the internal dome surface, most likely linked to the tiny geometrical
scale of the model.
Therefore no undue extrapolation of these curious results
should be done to full scale.

 ,
which creates weak convective
flows. Stronger convective flows from larger
,
which creates weak convective
flows. Stronger convective flows from larger 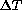 s
tend to predominate over external disturbances.
Some subsequent measurements were taken outside of working hours
in order to minimize disturbances that may affect "room turbulence",
which resulted in sequences - noted with 1) -
with substantially less mean seeing and variability.
Fig.
s
tend to predominate over external disturbances.
Some subsequent measurements were taken outside of working hours
in order to minimize disturbances that may affect "room turbulence",
which resulted in sequences - noted with 1) -
with substantially less mean seeing and variability.
Fig.