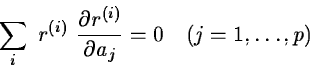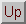



Next: The Modified Gauss-Newton Method.
Up: Outline of the Available
Previous: Outline of the Available
This is the simplest one.
The necessary condition for the function 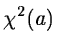 to have an extremum is that the partial derivatives vanish i.e.
to have an extremum is that the partial derivatives vanish i.e.
or, equivalently,
J(a)T r(a) =0 .
This is usually a system of non-linear equations that, numerically, can
be solved using the Newton-Raphson's method also called in the
one-dimensional case the tangents method.
The Taylor development of the function limited to the first order
is taken around some initial guesses of the parameters. The resulting
linear system
gives thus a correction to the solution
and
is taken as the new approximation of the optimum. The
relaxation factor 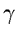 is a parameter of the method.
The convergence of the process towards the solution
of the non-linear minimization problem has been proven for locally
convex
is a parameter of the method.
The convergence of the process towards the solution
of the non-linear minimization problem has been proven for locally
convex 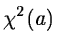 or under other assumptions impossible to detail here.
These conditions are not generally fulfilled in real problems. Moreover,
the algorithm ignores the second order conditions and therefore, may
end on a saddle point or never converge.
Two different relaxation factors may lead to different solutions or
one may give convergence and the other one not.
No general rule can be given for the choice of a good relaxation factor.
or under other assumptions impossible to detail here.
These conditions are not generally fulfilled in real problems. Moreover,
the algorithm ignores the second order conditions and therefore, may
end on a saddle point or never converge.
Two different relaxation factors may lead to different solutions or
one may give convergence and the other one not.
No general rule can be given for the choice of a good relaxation factor.




Next: The Modified Gauss-Newton Method.
Up: Outline of the Available
Previous: Outline of the Available
http://www.eso.org/midas/midas-support.html
1999-06-09