![[ ESO ]](/observing/etc/doc/images/eso-logo.gif)
![[ ESO ]](/observing/etc/doc/images/eso-logo.gif)
|
|
|---|---|
Infrared Exposure Time Calculator |
|
The ETC consists of two pages. The input page, presents the observation parameters the entry fields and widgets for the target information, expected atmospheric conditions, instrument configuration, observation parameters such as exposure time or signal-to-noise, and results selection. An "Apply" button submits the parameters to the model executed on the ESO Web server. The results page presents the computed results, including number of counts for the object and the sky, signal-to-noise ratios, instrument efficiencies, PSF size etc.. The optional graphs are displayed within Java applets allowing interactive manipulation. The results are also provided in ASCII and GIF formats for further analysis and printing. Finally a summary of the input parameters is appended to the result page.
Note: These tools are only provided for technical assessment of observation feasibility. Variations of the atmospheric conditions can strongly affect the required observation time. Calculated exposure time do not take into account instrument and telescope overheads. Users are advised to exert caution in the interpretation of the results and to report any result which may be suspected to be inconsistent.
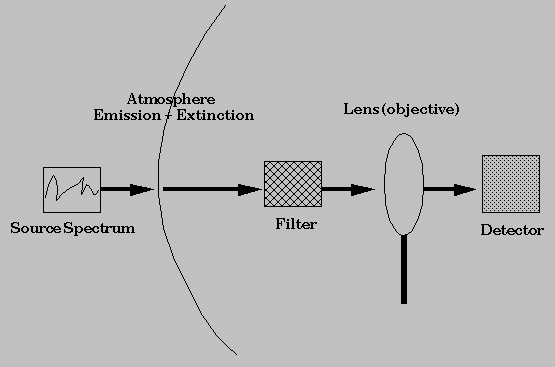
The exposure time calculator models the observation chain which includes the target spectral distribution, atmosphere parameters, instrument configuration, and detector setup. The following diagram illustrates the observation chain for imaging.
From the following, choose the spectrum shape you want for your target.
The flux density is constant at all wavelengths (F(lambda) = const.) The flux density level is determined from the specified object magnitude.
The target model is a blackbody defined by its temperature, expressed in Kelvin. The intensity distribution is scaled to the object magnitude.
Enter the J (1250 nm) , H (1650 nm), or Ks (2160 nm) magnitude closest in wavelength to the selected filter in imaging or the central wavelength of the defined spectrum (e.g. J if you choose J,Js or NB-1.187, H if you choose H or NB-1.644, Ks if you choose Ks of NB-2.122). In SOFI spectroscopy the blue grism is associated to J filter, and the red grism to the Ks filter. Information about the photometric filters and zero points is available here.
The input spectrum is a single emission line. It is an analytic Gaussian, centered on the wavelength parameter, defined by its total flux and full-width at half-maximum FWHM.
NB: When requesting a single line as input spectrum, the magnitude parameter is not taken into account. Only the line flux will be used to determine the signal magnitude.
NB: the fwhm of a single line shall not be smaller than 0.5nm. User-provided values smaller than this will be clipped to 0.5nm.
Point Source are sources whose spatial extend on the sky is much less than the seeing diameter. The signal to noise is computed over an area of diameter twice the Image Quality FWHM.
The signal to noise for extended sources is given per pixel on the detector. The magnitude is given per square arcsecond.
With the advent of instruments using new adaptive optics (AO) modes, new turbulence parameters need to be taken into account in order to properly schedule observations and ensure that their science goals are achieved. These parameters include the coherence time and the fraction of turbulence taking place in the atmospheric ground layer, in addition to the seeing. Starting from Period 105, the turbulence constraints are standardised to the turbulence conditions required by all instruments and modes, whether they are seeing-limited or AO-assisted.
The handling of atmospheric constraints thus changes for both Phase 1 (proposal preparation) and Phase 2 (OB preparation). In Phase 1, the seven current seeing categories are replaced by seven turbulence categories for all instruments. Each category can be defined by other parameters than a pure seeing threshold, depending on the instrument. For all instruments, all categories share the same statistical probability of realisation, which is key for an accurate time allocation process. In Phase 2, the image quality will still be the only applicable constraint for seeing-limited modes, whereas the same turbulence category as for Phase 1 will be used for diffraction-limited modes.
Users are encouraged to read the general description of these changes for Phase 1 and Phase 2 on the Observing Conditions webpage, as well as instrument User Manuals for specifics per instrument.
|
The definitions of seeing and image quality used in the ETC follow the ones given in Martinez, Kolb, Sarazin, Tokovinin
(2010, The Messenger 141, 5)
originally provided by Tokovinin (2002, PASP 114, 1156) but corrected by Kolb (ESO Technical Report #12):
Seeing is an inherent property of the atmospheric turbulence, which is independent of the telescope that is observing through the atmosphere; Image Quality (IQ), defined as the full width at half maximum (FWHM) of long-exposure stellar images, is a property of the images obtained in the focal plane of an instrument mounted on a telescope observing through the atmosphere. The IQ defines the S/N reference area for non-AO point sources in the ETC. With the seeing consistently defined as the atmospheric PSF FWHM outside the telescope at zenith at
500 nm, the ETC models the IQ PSF as a gaussian, considering the gauss-approximated transfer functions of the atmosphere, telescope and
instrument, with s=seeing, λ=wavelength, x=airmass and D=telescope diameter:
For fibre-fed instruments, the instrument transfer function is not applied. The diffraction limited PSF FWHM for the telescope with diameter D at observing wavelength λ is modeled as:
\(F_{\text{Kolb}} \) is the Kolb factor (ESO Technical Report #12):
|
The sky background model is based on the Cerro Paranal Advanced Sky Model,
also for instruments at la Silla, except for the different altitude above sea level. The observatory coordinates are automatically assigned for a given instrument.
By default, the airmass and moon phase parameters are entered manually. The sky model will use fixed typical values for all remaining relevant parameters (which can be seen in the output page by enabling the check box "show skymodel details").
Alternatively, a dynamic almanac widget can be enabled to facilitate assignment of accurate sky model parameters for a given target position and time of observation. The sky radiation model includes the following components: scattered moonlight, scattered starlight, zodiacal light, thermal emission by telescope and instrument, molecular emission of the lower atmosphere, emission lines of the upper atmosphere and airglow continuum.
The almanac is updated dynamically by a service on the ETC web server, without the need to manually update the web application.
Notes about the algorithms, resources and references for the almanac are available here. A more advanced version of the almanac is included in our SkyCalc web application, which provides more input and output options.
Hovering the mouse over an input element in the almanac normally displays a pop-up "tooltip" with a short description.
The upper left part of the almanac box refers to the date and time of observation.
This can be done with a UT time or a MJD. A date/time picker widget will appear when
the UT input field is clicked, but the UT can also be assigned manually. In any case, the
UT and MJD fields are dynamically coupled to be mutually consistent.
The two +/- buttons can be used to step forward or backward in time by the indicated step and unit per click. The buttons can be held down to step continuously until released.
The third of night corresponding to the currently selected time is indicated. This is an input parameter to the airglow component in the sky model. Twilight levels (civil, nautical and astronomical) referring to the sun altitude ranges are also indicated in the dynamic text. These levels refer to the sun altitude:
The target equatorial coordinates RA and dec can be assigned manually in the two input
fields or automatically using the SIMBAD resolver to retrieve the coordinates.
If the lookup is successful, an "info" link will open a window in which the raw SIMBAD response can be inspected.
The units can be toggled between decimal degrees and hh:mm:ss [00:00:00 - 23:59:59.999] for RA and dd:mm:ss (or dd mm ss) for dec. A whitespace can be used as separator instead of a colon.
The table dynamically displays the output from the server back-end service, including temporal and spatial coordinates for the target, Moon and Sun. The bold-faced numbers indicate the parameters normally relevant in the phase 1 proposal for optical instruments. The numbers appear in red color if they are out of the range supported by the sky model.
The chart dynamically shows the altitude and equivalent airmass as function of time for the moon and target,
centered on midnight for the currently selected date.
The green line, which refers to the currently selected time,
can be dragged left and right to change the time, dynamically coupled with the sections in the Time section.
Choosing the instrument filter determines in which band the observation will be performed. The magnitude parameters for object and sky are defined in the observation band you choose by choosing an instrument filter. It is not possible to define an input spectrum in J and observe it in Ks, for example.
The list of available objectives can be selected from the pull-down menu.
Objective Pixel Scale
SOFI Small field 0.144 arcsec/pixel
SOFI Large field 0.292 arcsec/pixel
Slits can be selected from the pull-down menu.
Remember to select the correct low or medium resolution option.
The Exposure Time Calculator is made of 2 interactive Web forms. Fill in the input form to define the kind of object you want to observe, the atmospheric conditions, instrument and detector setups. Set a Signal to Noise Ratio (SNR) to achieve and get an Exposure Time estimation, or the opposite: given a DIT, NDIT and NINT (i.e. exposure time), estimate the SNR you would get.
The output form will give you estimates for SNR or Exposure Time, together with graphs you selected for output. These graphs are interactive Java applets which may require that you setup your browser to activate them. Help can be found from the output page about how to use the Java applets.
To set up the observation, either a SNR or an exposure time must be user-defined. The simulation computes then the associated value.
Indicate here a value of the Signal to Noise Ratio (SNR) and get an estimation of the exposure time required to achieve it.
Non-chopping is only offered in the following modes:
For the chopping mode, the user selects the total exposure time, in minutes. The DIT (Detector Integration Time) depends of the instrument configuration. The NDIT (Number of Detector InTegrations) is then found from the total exposure time, by dividing with the DIT.
Detector on-chip integration time (in seconds).
Exposure Time for an infra-red detector is the product of DIT and NDIT and NINT. For chopping modes, the DIT is fixed and NDIT is found from the total exposure time (NINT is 1).
The total exposure time is therefore DIT x NDIT x NINT.
Toggling this option will display the object spectrum as seen by the detector.
Toggling this option will display a curve showing the evolution of Signal to Noise Ratio as a function of Exposure Time.
This option will display a curve showing the total efficiency of the system, excl. the atmospheric absorption.
Toggling this option will display a curve showing the evolution of Signal to Noise Ratio against seeing in arcseconds.
The input flux distribution is displayed in units of 1e-20 ergs/cm**2/s/A
The sum of the object signal and the sky background spectrum for the central row of the spectrum.
The total integrated counts contribution from the object, in e-/pixel/DIT
The sky contribution on each row of the detector, in e-/pixel/DIT.
Toggling this option will display a curve showing the evolution of Signal to Noise Ratio against wavelength.
This option will display a curve showing the total efficiency of the system, excl. the atmospheric absorption.
The input flux distribution is displayed in units of ergs/cm2s/A
| Send comments and questions via https://support.eso.org/ |