3-way beam combiner

Fringe parameters are the complex visibility, the squared visibility amplitude, and the total count rate. These can be computed from bincounts using the functions fringevis, fringevissq, and fringenphot.

v=fringevis(bincounts(1,*,*,*))
v2=fringevissq(bincounts(1,*,*,*))
help,v,v2

V COMPLEX = Array[32, 42300]
V2 DOUBLE = Array[32, 42300]

A complex variable has real and imaginary parts, they can be plotted as follows.

window,xsize=400,ysize=400
plot,float(v(0,*)),imaginary(v(0,*)),psym=3,xrange=[-50,50],yrange=[-50,50]

?


Instead of computing the modulus of the complex visibility, we use a different estimator for the squared amplitude. The reason for this is not trivial, but has to do with obtainig an unbiased estimate of of the amplitude.

window_slide plot,v2(0,*),psym=3



6-way beam combiner

Note that the data shown below are actually using only three stations, but the encoding and hardware used were the new NPOI six-station configuration.

Fringe spectrum analysis

Here I analyse the (squared) fringe amplitude of channel 1 as a function of k, the Fourier (frequency) variable conjugate to the Bin index. From the fringe frame data for a scan I derive the photonrate N and then, after subtracting the mean photonrate/bin level, I derive X^2+Y^2-N by direct Fourier transform, using 2*pi*j*k/64 as the phase interval. Nominator and denominator (N^2) are then averaged 500 samples at a time, then divided, and averaged again. The result is multiplied with 4/sinc(k/n)^2 for normalization. I have verified with simulated fringe frames that this procedure results in the correct squared visibility amplitudes.

Using the observer star and obs log sheets to figure out which tracking was selected and which stations were pointed at the star, I check whether I find fringe frequency peaks at positions (i.e. values of k) consistent with that information.

Here is the configuration information from which we can see what baselines correspond to which values of k: 

print,genconfig.stationid
	E02 AC0 AE0 AW0 W07 AN0                                                                                      
print,genconfig.fringemod
           7           1           6           5           2           8
           5           3           7           4           1           8
print,genconfig.baselineid
      E02-AE0 AE0-AW0 AN0-AW0 AN0-AE0 E02-AN0 E02-AW0
      E02-AC0 AC0-AW0 W07-AW0 W07-AC0 E02-W07 E02-AW0

The fringemod parameter indicates the values of k, the first line above corresponding to the first spectrometer. The baselines by spectrometer are also given above.
Here is the fringe frequency spectrum for scan 6 on 2001-10-16 while E02, AC0, and AW0 were tracking a star. The spectrum below shows that we indeed see peaks at k=3 (AC0-AW0), 5 (E02-AC0), and 8 (AW0-E02)


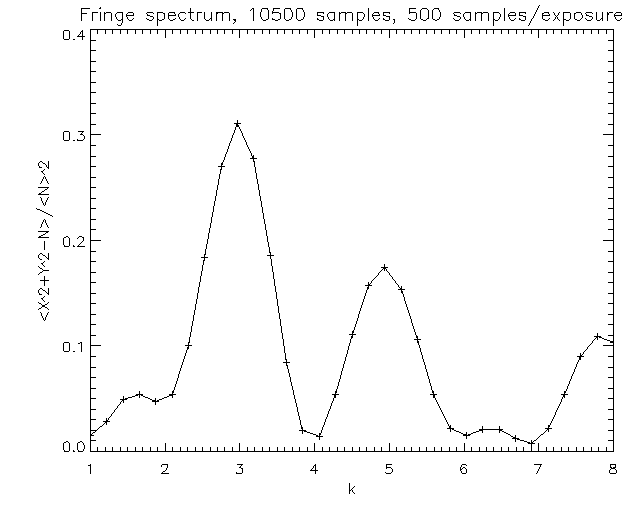
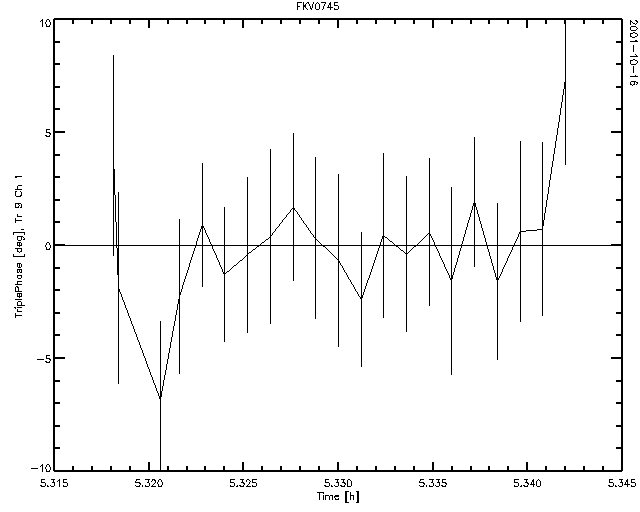
The one-second averaged closure phase derived for the three baselines in this spectrometer is shown below. It is of good quality and clearly free of atmospheric phase noise.


The third baseline occurs twice in this configuration, and the same triple, but in a sense independent from the first one, can be computed and is shown here.